인덱스 트리
인덱스 트리는 값이 계속 변경되는 구간의 대표값을 구할 때 쓰이는 자료구조이다. 여기서 대표값이란 구간의 합, 최솟값, 최댓값 등을 말한다. 이번 글에서는 구간의 합을 예시로 들어 설명하겠다.
인덱스 트리의 구조
인덱스 트리에서 부모 노드는 자식 노드의 대표값을 가진다. 아래와 같은 노드가 있다고 해보자.

이 노드들의 부모는 어떤 값을 가질까? 루트 노드까지 트리를 채워보자.

부모 노드는 자식 노드의 합이라는 것을 볼 수 있다. 여기서 주의해야 하는 점은 이진 트리의 각 계층은 2의 제곱수만큼 노드를 가져야 하는데, 우리 예시는 노드가 5개 뿐이다. 즉, 5보다 큰 2의 제곱수인 8보다 3개 모자르다. 따라서 현재 우리는 구간의 합을 구하는 문제이기 때문에 합에 영향을 끼치지 않는 0으로 채워준다.
만약 구간의 합이 아닌 최솟값이라면 최솟값에 영향을 미치지 않는 매우 큰 값 ex) Integer.MAX_VALUE, 구간의 곱이라면 1 이렇게 채워주면 될 것이다.
값이 변경되는 경우
앞에서 말햇듯이 인덱스 트리는 값이 계속 변경되는 경우 유용하게 쓰이는 자료구조이다. 만약 {1, 2, 3, 4, 5} 중 1을 8로 바꾸면 트리에 어떤 일이 생길지 생각해보자.
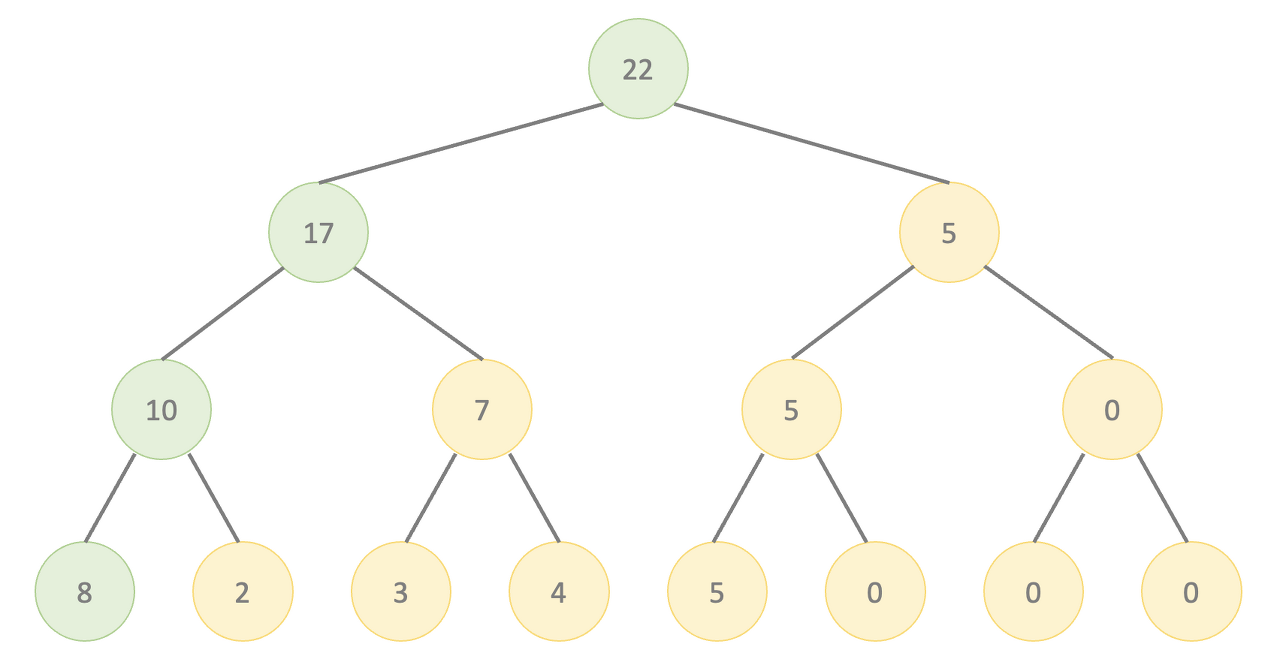
값이 변경된 노드와 부모-자식 혹은 조상-손자(맞나..?) 관계를 가지는 노드들의 값도 변화가 발생한다.
코드
private static void update(int idx, long value) {
tree[offset + idx] = value;
int i = (offset + idx) / 2;
while(i >= 1) {
tree[i] = tree[i * 2] + tree[i * 2 + 1];
i /= 2;
}
}여기서 offset은 트리의 마지막 층이 시작되는 인덱스를 말한다. 위와 같은 트리에서는 offset = 8이다.
구간 합 구하기
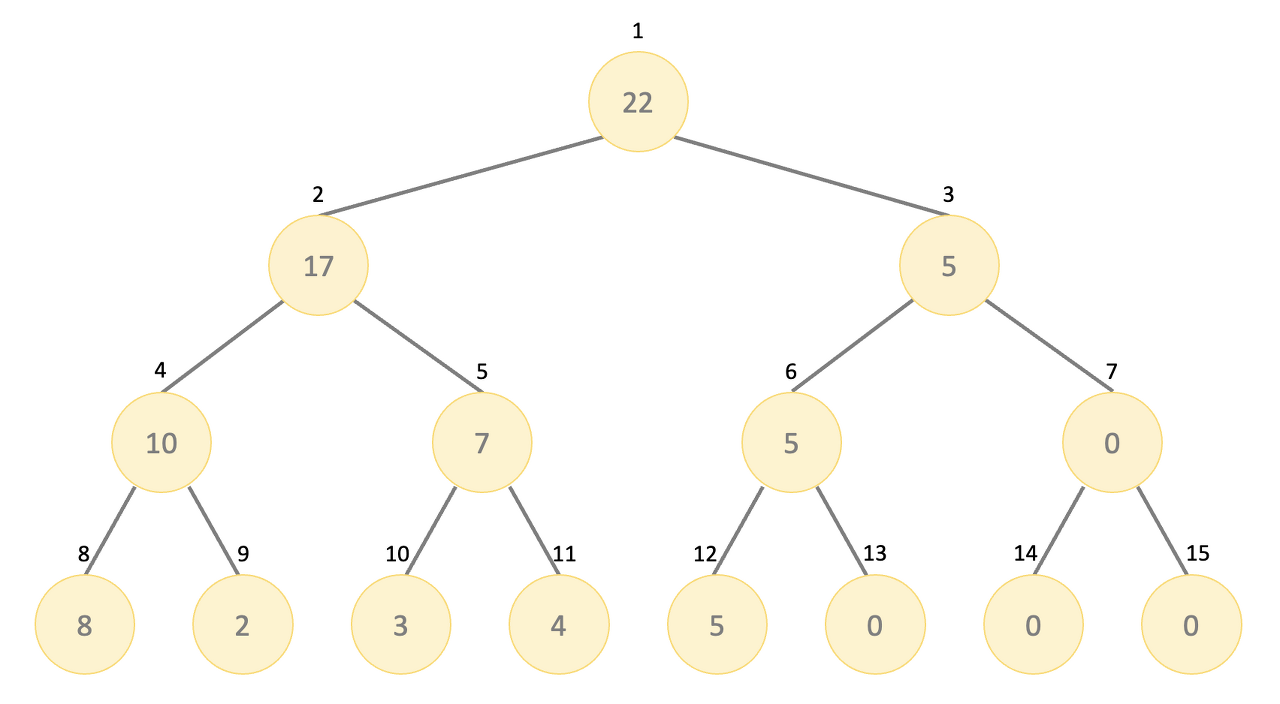
세번째 ~ 네번째의 구간 합을 구해보자. 두 노드의 부모 노드가 같고, 두 구간의 합을 나타내기 때문에 구간 합 7을 쉽게 구할 수 있다.
만약 두번째~다섯번째까지의 구간합을 구하는 경우는 어떨까?
두번째 노드의 부모 및 조상들은 첫번째 노드의 합도 포함하고 있다. 따라서 두번째 노드와 연결된 노드들은 필요 없다.
다섯번째 노드도 마찬가지로 부모 및 조상들이 여섯번째 노드의 합도 포함하고 있기 때문에 다섯번째 노드와 연결된 노드들은 필요 없다.
여기서 한 가지 사실을 알 수 있다.
시작 노드의 인덱스가 홀수인 경우 해당 노드와 연결된 노드들은 필요없다. 마찬가지로 끝 노드의 인덱스가 짝수인 경우 해당 노드와 연결된 노드들은 필요없다.
코드
private static long sum(int start, int end) {
start += offset;
end += offset;
long sum = 0;
while(start <= end) {
// 시작 점이 오른쪽(홀수)인 경우
if(start % 2 != 0) {
sum += tree[start++];
}
// 끝 점이 왼쪽(짝수)인 경우
if(end % 2 == 0) {
sum += tree[end--];
}
start /= 2;
end /= 2;
}
return sum;
}구간 합이 int 범위를 넘어갈 수 있으므로 long으로 선언해주었다.
'Study > Algorithm' 카테고리의 다른 글
| 최장 증가 부분 수열(LIS) (0) | 2025.04.04 |
|---|---|
| 유니온 파인드 (Union-Find) (0) | 2023.10.03 |
| 분할 정복 (Divide and Conquer) (0) | 2023.08.17 |
| 이분탐색을 활용한 Lower bound, Upper bound (0) | 2023.08.07 |
| 이분 탐색 (Binary Search) (0) | 2023.08.06 |